Что означает уклон в процентах, и как перевести его в градусы
Когда идет речь о кровле зданий, то под словом «уклон» подразумевают угол наклона оболочки крыши к горизонту. В геодезии данный параметр является показателем крутизны склона, а в проектной документации это степень отклонения прямых элементов от базовой линий. Уклон в градусах не вызывает ни у кого вопросов, а вот уклон в процентах порой вызывает замешательство. Пришла пора разобраться с этой единицей измерения, чтобы четко представлять себе, что это такое и, если потребуется, без особого труда переводить ее в другие единицы, например в те же градусы.
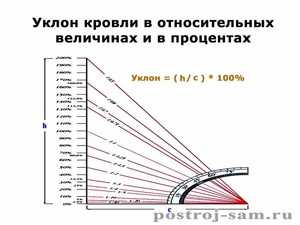
Расчет уклона в процентах
Попробуйте представить прямоугольный треугольник АВС, лежащей на одном из своих катетов АВ. Второй катет ВС будет направлен вертикально вверх, а гипотенуза АС образует с нижним катетом некий угол. Теперь нам предстоит немножко вспомнить тригонометрию и рассчитать его тангенс, который как раз и будет характеризовать уклон, образуемый гипотенузой треугольника с нижним катетом. Предположим, что катет АВ = 100 мм, а высота ВС = 36,4 мм. Тогда тангенс нашего угла будет равен 0,364, что по таблицам соответствует 20˚. Чему же тогда будет равен уклон в процентах? Чтоб перевести полученное значение в эти единицы измерения, мы просто умножаем значение тангенса на 100 и получаем 36,4%.
Как понимать угол уклона в процентах?
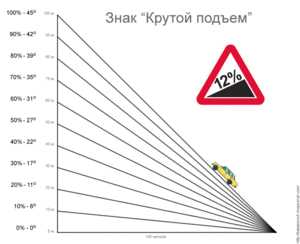
Если дорожный знак показывает 12%, то это означает, что на каждом километре такого подъема или спуска дорога будет подыматься (опускаться) на 120 метров. Чтобы перевести процентное значение в градусы, нужно попросту вычислить арктангенс этого значения и при необходимости перевести его из радиан в привычные градусы. То же самое касается и строительных чертежей. Если, к примеру, указывается, что угол уклона в процентах равен 1, то это означает, что соотношение одного катета к другому равно 0,01.

Почему не в градусах?
Многих наверняка интересует вопрос: «Зачем для уклона использовать еще какие-то проценты?» Действительно, почему бы просто не обойтись одними градусами. Дело в том, что при любых измерениях всегда имеет место некоторая погрешность. Если в проектной документации станут применять градусы, то неминуемо возникнут сложности с монтажом. Взять хотя бы ту же канализационную трубу. Погрешность в несколько градусов при длине в 4-5 метров может увести ее совершенно в другую от нужного положения сторону. Поэтому в инструкциях, рекомендациях и проектной документации обычно применяются проценты.
Применение на практике
Предположим, что проект строительства загородного дома предполагает устройство скатной кровли. Требуется проверить ее уклон в процентах и градусах, если известно, что высота конька составляет 3.45 метра, а ширина будущего жилища равна 10 метрам. Так как спереди крыша представляет собой равносторонний треугольник, то ее можно разделить на два прямоугольных треугольника, в которых высота конька будет являться одним из катетов. Второй катет находим, разделив ширину дома пополам.
 Теперь у нас есть все необходимые данные для расчета величины уклона. Получаем: atan-1(0.345) ≈ 19˚. Соответственно, уклон в процентах равен 34,5. Что нам это дает? Во-первых, мы можем сравнить это значение с рекомендуемыми специалистами параметрами, а во-вторых, свериться с требованиями СНиПа при выборе кровельного материала. Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.
Теперь у нас есть все необходимые данные для расчета величины уклона. Получаем: atan-1(0.345) ≈ 19˚. Соответственно, уклон в процентах равен 34,5. Что нам это дает? Во-первых, мы можем сравнить это значение с рекомендуемыми специалистами параметрами, а во-вторых, свериться с требованиями СНиПа при выборе кровельного материала. Сверившись со справочниками, можно выяснить, что для укладки натуральной черепицы такой уровень наклона будет слишком малым (минимальный уровень равен 33 градусам), зато такой крыше не страшны мощные порывы ветра.fb.ru
Уклон 12%, сколько это в градусах?
12% от 90 градусов.
360 — 100%, дальше сам
примерно 7 град
Уклон дороги — относительное превышение одной точки продольного (поперечного) профиля дороги над другой, определяемое как отношение превышения к горизонтальному расстоянию между двумя точками. Уклон 10% Это отношение высоты подъёма в 10 метров к горизонтальной проекции дороги длинной 100метров. В геометрическом смысле — это тангенс угла подъёма дороги. Чтобы перевести уклон из процентов в градусы надо уклон дороги в процентах разделить на100 и полученную велину посмотреть в таблице Брадиса раздел Тангенсы. <a href=»/» rel=»nofollow» title=»11898030:##:http://www.webmath.ru/poleznoe/table_tg.php» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a> Для уклона 10% угол уклона в процентах будет примерно tg(6°) -0.105 Шесть градусов. Для уклона 100% угол наклона 45 градусов.
Это надо понимать также, как говорят: скидка цен на товары 40%, спрашивается от двух милионов скидывают или от трёх, а другой спрашивает, с какого этажа скидывают с пятого или с девятого?
Уклон в процентах часто используют для обозначения уклона дорог или строительных объектов. Нулевой уклон означает горизонтальную поверхность. Уклон в 100% означает подъём на 1 метр на каждый метр расстояния, т. е. угол наклона 45 градусов. Вертикальная линия имеет бесконечное значение уклона.
12% — 5.4 градуса. Процент считается от 45%.
Мозги людям пудрите, арктангенс (12%/100%)=6,84
touch.otvet.mail.ru
| 1 | Вычислить | 2+2 | |
| 2 | Вычислить | ||
| 3 | Вычислить | 4^2 | |
| 4 | Разложить на простые множители | 73 | |
| 5 | Вычислить | 6/2(1+2) | |
| 6 | Найти объем | сфера (5) | |
| 7 | Найти площадь | окружность (5) | |
| 8 | Вычислить | корень четвертой степени -625 | |
| 9 | Вычислить | -5^2 | |
| 10 | Вычислить | 2^4 | |
| 11 | Найти площадь поверхности | сфера (5) | |
| 12 | Вычислить | -3^2 | |
| 13 | Вычислить | 2^5 | |
| 14 | Вычислить | 6÷2(1+2) | |
| 15 | Вычислить | 3^2 | |
| 16 | Преобразовать в десятичную форму | 1/4 | |
| 17 | Вычислить | (-3)^3 | |
| 18 | Вычислить | -2^2 | |
| 19 | Вычислить | 2^2 | |
| 20 | Вычислить | 6^2 | |
| 21 | Вычислить | квадратный корень 3* квадратный корень 12 | |
| 22 | Вычислить | (-4)^2 | |
| 23 | Вычислить | -7^2 | |
| 24 | Преобразовать в десятичную форму | 3/4 | |
| 25 | Преобразовать в десятичную форму | 7/8 | |
| 26 | Вычислить | квадратный корень 28+ квадратный корень 63 | |
| 27 | Преобразовать в десятичную форму | 2/3 | |
| 28 | Найти площадь | окружность (7) | |
| 29 | Найти площадь | окружность (2) | |
| 30 | Вычислить | 8^2 | |
| 31 | Разложить на простые множители | 6 | |
| 32 | Преобразовать в обыкновенную дробь | 0.75 | |
| 33 | Вычислить | — корень четвертой степени 625 | |
| 34 | Найти площадь | окружность (4) | |
| 35 | Преобразовать в десятичную форму | 3/8 | |
| 36 | Вычислить | 4^3 | |
| 37 | Разложить на простые множители | 8 | |
| 38 | Вычислить | 5^3 | |
| 39 | Преобразовать в десятичную форму | 3/8 | |
| 40 | Найти площадь | окружность (6) | |
| 41 | Преобразовать в десятичную форму | 3/4 | |
| 42 | Вычислить | (-4)^3 | |
| 43 | Вычислить | 3^3 | |
| 44 | Разложить на простые множители | 4 | |
| 45 | Найти объем | сфера (4) | |
| 46 | Перевести в процентное соотношение | 1/8 | |
| 47 | Найти площадь | окружность (3) | |
| 48 | Преобразовать в десятичную форму | 2/5 | |
| 49 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 50 | Вычислить | 5^2 | |
| 51 | Вычислить | (-2)^4 | |
| 52 | Разложить на простые множители | 2 | |
| 53 | Вычислить | корень четвертой степени 256 | |
| 54 | Вычислить | квадратный корень 81 | |
| 55 | Преобразовать в десятичную форму | 1/2 | |
| 56 | Вычислить | -4^2 | |
| 57 | Вычислить | -9^2 | |
| 58 | Вычислить | (-5)^2 | |
| 59 | Вычислить | (-8)^2 | |
| 60 | Разложить на простые множители | 741 | |
| 61 | Разложить на простые множители | 9 | |
| 62 | Найти объем | сфера (3) | |
| 63 | Вычислить | 3 квадратный корень 8*3 квадратный корень 10 | |
| 64 | Найти площадь | окружность (10) | |
| 65 | Найти площадь | окружность (8) | |
| 66 | Вычислить | -8^2 | |
| 67 | Вычислить | (-5)^3 | |
| 68 | Вычислить | (-2)^3 | |
| 69 | Вычислить | 10^6 | |
| 70 | Вычислить | 10^2 | |
| 71 | Вычислить | -6^2 | |
| 72 | Преобразовать в десятичную форму | 1/5 | |
| 73 | Преобразовать в десятичную форму | 4/5 | |
| 74 | Преобразовать в десятичную форму | 10% | |
| 75 | Найти площадь поверхности | сфера (6) | |
| 76 | Перевести в процентное соотношение | 3/5 | |
| 77 | Вычислить | (-2)^2 | |
| 78 | Разложить на простые множители | 12 | |
| 79 | Разложить на простые множители | 1162 | |
| 80 | Вычислить | 6^3 | |
| 81 | Вычислить | -3^4 | |
| 82 | Вычислить | 2^2 | |
| 83 | Вычислить | (-6)^2 | |
| 84 | Вычислить | (-7)^2 | |
| 85 | Найти площадь | окружность (1) | |
| 86 | Преобразовать в десятичную форму | 2/5 | |
| 87 | Вычислить | квадратный корень 2+ квадратный корень 2 | |
| 88 | Вычислить | 2^1 | |
| 89 | Вычислить | 2^6 | |
| 90 | Разложить на простые множители | what is the prime factoriztion of 40 use exponents to show any repeated prime factors | what is the prime factoriztion of use exponents to show any repeated prime factors |
| 91 | Вычислить | -2^3 | |
| 92 | Вычислить | 3^5 | |
| 93 | Вычислить | (-9)^2 | |
| 94 | Вычислить | 4^1 | |
| 95 | Вычислить | квадратный корень 100 | |
| 96 | Преобразовать в десятичную форму | 25% | |
| 97 | Найти длину окружности | окружность (5) | |
| 98 | Найти площадь поверхности | сфера (6) | |
| 99 | Найти объем | сфера (2) | |
| 100 | Найти объем | сфера (6) | |
www.mathway.com
Уклон в градусах и процентах
Горнолыжные градиенты или о крутизне синих, красных и черных трасс
Поговорим об уклонах
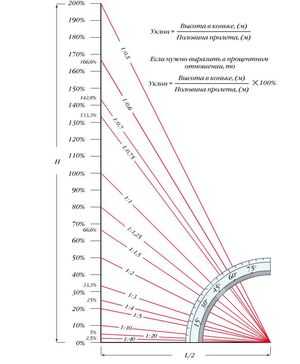
На практике крутизна наклонной поверхности в различных областях человеческой деятельности обозначается величиной уклона (или еще иначе — градиентом). Для начала давайте разберемся, что же означает само это понятие. Таблички с указанием уклона знакомы, наверное, всем водителям автомобилей (по крайней тем, кто самостоятельно сдал хотя бы теорию), но далеко не все из них знают, что же фактически означает, например, 10% на знаке.
Кто-то по-простому думает, что это угол наклона дороги, то есть 10 градусов. Некоторые идут дальше в своих размышлениях и считают, что это доля от максимально возможного угла подъема в 90 градусов (отвесная стена) и 10% — это 90°×0.1 = 9°. Мы все привыкли мыслить в градусах, каждый может визуально представить себе 90 градусов, 45, 30 и т.д., поэтому и стремимся все воспринимать в этой единице измерения (а правильный ответ: 10% = 5.7°).
На самом деле математически уклон — это отношение перепада высоты на определенном участке пути к длине горизонтальной проекции этого пути, выраженное в процентах. Т.е. высота (h), разделенная на проекцию пути (c) и умноженная на 100. Геометрически это отношение противолежащего катета к прилежащему (тангенс, умноженный на 100). Таким образом:
Уклон в процентах (градиент) = h/c×100 = tg(a)×100
Ниже представлена форма, позволяющая перевести значения из градиентов в градусы и обратно:
Градиенты % = Градусы °
Ближе к делам горнолыжным
С теорией разобрались, переходим к горнолыжной практике.
Профиль горнолыжной трассы никогда не представляет из себя идеальную прямую. Где-то наклон может быть покруче, где-то поположе.
Уклон кровли в градусах и процентах
В этом случае используется понятие среднего градиента, который, впрочем, вычисляется все по той же формуле: перепад высот между стартом и финишем трассы, деленный на длину горизонтальной проекции трассы.
По статистике средние градиенты синих трасс находятся в пределах до 18% (порядка 10 градусов), красных — до 23% (13 градусов), а черных — от 23% и выше (больше 13 градусов). На каких-то курортах сложность трасс несколько занижена (синие трассы в реальности могут оказаться ближе к красным по крутизне), на каких-то наоборот, ее завышают, но в среднем картина везде примерно такая.
Для ориентировочной оценки длин трасс, катаясь на курорте и имея на руках схему катания с обозначением перепадов высот, вы можете использовать следующие соотношения:
На каждый километр перепада высоты синей трассы приходится порядка 7 км ее длины, на километр перепада красной — 5 км, черной — 3.5 км.
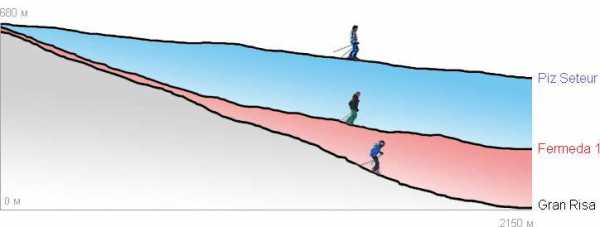
Ниже на картинке для сравнения представлены профили синей, красной и черной трасс. Трассы находятся в известнейшем итальянском регионе Селларонда, а профили их взяты из замечательного приложения 3D Dolomiti Superski, которое позволяет совершить виртуальный тур по региону, а также посмотреть технические характеристики всех трасс.

| Название трассы | Длина | Перепад | Наклон | Градиент |
|---|---|---|---|---|
| Piz Seteur | 2050 м | 204 м | 5.7° | 10.0% |
| Fermeda 1 | 2090 м | 456 м | 12.6° | 22.4% |
| Gran Risa | 2290 м | 677 м | 17.2° | 30.9% |
Отдельно отметим представленную на картинке Gran Risa — знаменитую трассу, входящую в пятерку культовых трасс Кубка мира. Глядя на ее профиль можно подумать, что ничего такого особенного в нем нет, но на деле, когда вы оказываетесь на трассе, в некоторых местах может показаться, что склон уходит вертикально вниз.
Этот эффект часто присутствует при сравнении профиля трассы с реальной обстановкой на местности. Также не будем забывать, что мы все время ведем речь о средних градиентах, в то время как некоторые локальные участки склона могут оказаться намного круче (и часто именно по этим самым крутым местам присваивают сложность трассе).
Харакири
В австрийском Майрхофене находится одна из самых крутых трасс мира (и самая крутая в Австрии), с говорящим названием Harakiri. Ее средний уклон составляет 78% (38°, длина около 620 метров при перепаде 380 метров). Для подготовки склона используется специальная техника, закрепленная на спущенных сверху страховочных канатах.

Падение на Harakiri может быть чревато тем, что до конца трассы вы будете катиться кубарем, не имея возможности затормозить.
Так что всегда, катаясь на лыжах, соизмеряйте свои возможности с предлагаемыми горами условиями. Берегите себя и окружающих лыжников!
  При решении геодезических и инженерных задач, очень часто приходиться вспоминать и искать необходимые формулы. В связи с этим хочется представить Вам шпаргалку (назовем её “геодезической шпаргалкой”:)), в которой приведены часто использующиеся формулы.
  Конечно, ее содержание не охватывает всю высшую математику или сферическую геометрию, но что-нибудь должно пригодиться.
  Зная из собственного опыта, неудобство восприятия формул без чисел, к каждой из них приводится пример вычисления.
Пример вычислений теорема Пифагора
Пример вычислений соотношения в прямоугольном треугольнике
— арксинус (arcsin) возвращает угол по его синусу
— арккосинус (arccos) возвращает угол по его косинусу
— арктангенс (arctg) возвращает угол по его тангенсу
— арккотангенс (arcctg) возвращает угол по его арктангенсу
Пример вычислений обратные тригонометрические функции
Сумма углов в треугольнике равна 180 градусам
Для любого треугольника соблюдается выражение
Пример вычислений теорема синусов
  Квадрат любой стороны треугольника, равен сумме квадратов двух других его сторон, минус удвоенное произведение этих сторон на косинус угла между ними
Пример вычислений теорема косинусов
  Площадь треугольника можно определить по формулам
также удобно использовать формулу Герона , где p-полупериметр треугольника
Пример вычислений площадь треугольника
или по формуле Герона
  Длина дуги окружности вычисляется по формулам
если угол задан в угловых градусах минутах и секундах
если угол задан в радианах
Пример вычислений длина дуги окружности
угол задан в угловых градусах минутах и секундах
угол задан в радианах
  Перевод угловых градусов минут и секунд в градусы выполняется согласно выражения
Пример вычислений
перевести в градусы угол, который задан в угловых градусах минутах и секундах
Смотрите перевод минут и секунд угла в градусы онлайн   Перевод градусов в угловые градусы минуты и секунды выполняется согласно выражения
Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в градусах
Смотрите перевод градусов угла в минуты и секунды онлайн   Перевод градусов в радианы выполняется по формуле
Пример вычислений
перевести в радианы угол, который задан в угловых градусах минутах и секундах
Смотрите перевод градусов в радианы онлайн   Перевод радианов в градусы выполняется по формуле
Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в радианах
Смотрите перевод радиан в градусы онлайн   Определение наклона линии в градусах выполняется с использованием соотношений в прямоугольном треугольнике Пример вычислений
  Определить наклон пандуса длиной 14м и высотой 3,5м
  При инженерно-строительных работах, наклон линии задают не градусом наклона, а тангенсом этого градуса — безразмерной величиной, которая называется уклоном. Уклон может выражаться относительным числом, в процентах (сотые доли числа) и промилле (тысячные доли числа)
Пример вычислений
  Определить уклон отмостки длиной 2,5м и высотой 0,30м
astgift.ru
Проценты на дорожном знаке — важное предупреждение? | Авто-мото
Вы уже обращали внимание на предупреждающие дорожные знаки с черным треугольником, символизирующим спуск или подъем, и количеством процентов, обозначающим крутизну этого спуска (или подъема)? И, возможно, задавали себе вопрос — а, например, 12% — это сколько? И почему бы крутизну уклона не обозначать в градусах?
На этих знаках обозначен тангенс угла наклона, выраженный в процентах.
Ну вот, ваша улыбка увяла, словно, развернув пакет с подарком, вы обнаружили в нем увесистый том Достоевского. А ведь уже через несколько минут вы будете непринужденно оперировать понятием «тангенс», а заодно «синус» и «косинус», удивляясь тому, что до сегодняшнего дня они заставляли вас напрягаться.
Итак, прислоните лыжную палку углом к стене напротив яркой лампы. Вы увидите две тени — одну на стене, другую на полу. Учителя, чтобы вас позлить, называли эти тени проекциями. Соответственно, на вертикальную и горизонтальную плоскости. Та тень, что на стене, называется «синус», та, что на полу — «косинус».
Чем ближе к стене вы придвинете низ палки, тем короче будет «косинус». Наоборот, отодвигая низ палки от стены, вы увидите, что «синус» становится все меньше, а «косинус» — больше. Отношение синуса к косинусу называется тангенсом.
Если вы установите палку под углом 45 градусов от пола, синус и косинус будут совершенно одинаковы. В таком случае тангенс будет равен 1. Или, как говорили ваши учителя, тангенс 45 градусов равен 1.
Если мы посмотрим сбоку на дорогу, в том месте, где она имеет уклон, то увидим, что угол этого уклона находится в пределах 8 градусов от горизонта. Высота подъема, или «синус», гораздо меньше, чем длина проекции дороги на горизонтальную плоскость — «косинус». Разделив высоту подъема на длину горизонтальной проекции, обнаружим, что тангенс угла такого уклона не превышает 0,12.
Его удобно выражать в процентах — например, 12%. В таком случае тангенс угла 45 градусов равен 100%.
Теперь вы уже смело можете использовать эту информацию. Так, проехав 1 километр по дороге с уклоном 12%, вы подниметесь (или спуститесь) на 120 метров. (При таких небольших углах уклона длину горизонтальной проекции дороги можно считать равной длине дороги).
Из любопытства вы можете перевести угол уклона обратно в градусы с помощью калькулятора на сотовом телефоне, настроив его на «научный» режим, например: TAN-1(0,12)=7 градусов. В некоторых калькуляторах: ATAN (0,12)=7.
Впрочем, для автолюбителей главное не это. Надеюсь, вы уже прочли мою статью о коэффициенте сцепления.
Так вот, оказывается, тангенс угла наклона равен коэффициенту сцепления.
Например, автомобиль, стоящий на сухом асфальтированном уклоне с коэффициентом сцепления 0,7, начнет сползать вниз, если тангенс угла наклона при этом будет равен 70% (Это уклон около 35 градусов, вряд ли вы когда-нибудь встретите такой.)
Но, кроме дорог, существуют улочки старых городов, особенно приморских, с углами наклона, существенно превышающими всевозможные нормативы. Так, при движении в сырую погоду вниз по асфальтированному уклону крутизной 20% эффективность торможения падает наполовину.
И очень часто вам придется двигаться по мокрому льду с коэффициентом сцепления 0,1 и менее. А это значит, что вы должны внимательно отслеживать предупреждающие дорожные знаки с черным треугольником и цифрами внутри. Их устанавливают, когда тангенс угла уклона приближается к 10%. Если вы пренебрежете этими знаками и остановитесь на подъеме, то в лучшем случае — не сможете сдвинуться с места. А уж если затормозите на спуске…
Но я убежден, что теперь ничего такого с вами не случится. И от души надеюсь, что сегодня хоть чуточку помог вам, дорогие матери — наша самая ответственная и любимая часть человечества.
shkolazhizni.ru
как рассчитать по формуле, СНИП
Выбирать уклон кровли только исходя из своих эстетических предпочтений было бы несколько опрометчиво. Поскольку надежность и прочность будущей конструкции во многом зависят от правильно рассчитанной величины угла наклона, учитывающей климатические особенности местности. То есть, уклон крыши должен быть оптимальным как с практической, так и с эстетической точки зрения.
То что идеально «плоских» крыш просто не может быть не подлежит сомнению. Ведь должна же дождевая вода каким-то образом отводиться с нее. Поэтому на них делают разуклонку, чтобы получить хотя бы минимальный уклон плоской кровли.
Она обеспечивает возможно эффективный сбор дождевой воды с поверхности кровельного покрытия и направляет ее либо к парапету, либо к внутренним воронкам.
| Вид кровельного покрытия | Вес 1 м.кв,кг | Безразмерный уклон крыши | Процентная мера уклона | Величина уклона в градусах |
| Шифер (среднего профиля/усиленного профиля) | 11/13 | 1:10 / 1:5 | 10% / 20% | 6° / 11,5° |
| Целлюлозно-битумные листы | 6 | 1:10 | 10% | 6° |
| Профнастил (однофальцевый) | 3-6,5 | 1:4 | 25% | 14° |
| Мягкая рулонная кровля | 9-15 | 1:10 | 10% | 6° |
| Профнастил (двухфальцевый) | 3-6,5 | 1:5 | 20% | 11,5° |
| Металлочерепица | 5 | 1:5 | 20% | 11,5° |
| Керамическая черепица | 50-60 | 1:5 | 20% | 11,5° |
| Цементная черепица | 45-70 | 1:5 | 20% | 11,5° |
минимальный угол наклона крыши
Минимальный уклон кровли зависит от многих параметров, включая материал гидроизоляционного покрытия, типа самой крыши (стандартная или инверсионная), количества гидроизоляционных слоев и другого.
Основные требования, определяющие уклон плоской кровли: СНИП ↑
Каким будет минимальный уклон кровли, в зависимости различных факторов диктуют специальные строительные правила и нормы.
Зависимость угла наклона крыши от гидроизоляции регулирует п. 4.3 СП 17.13330 за 2011 год, согласно которому уклон плоской кровли изменяется в интервале 1,5–10%. Большие углы (до 24%) выполняют крайне редко, поскольку выбор материала для гидроизоляции, который не сползал бы к основанию покатой кровли при повышении температуры, очень затруднителен.
На заметку
Наименьший уклон для плоской кровли равен 1.5% или 1°.
Как правило, кровля с малым уклоном имеет довольно большую площадь поверхности и добиться его идеального значения весьма проблематично. Наверняка останутся участки, где будет застаиваться вода, что может стать причиной износа кровельного материала или протечек. Относительно точно можно выполнить геометрию уклона при помощи стяжки. Возможно также использовать заливку из полистиролбетона или пенобетона. Для повышения прочности поверх уложенного слоя делают уже тонкий слой прочной бетонной стяжки.
В свою очередь, существует конкретная связь между крутизной кровельной конструкции и количеством слоев гидроизоляции. Чем больше она будет, тем вода, естественно, уходит быстрее, а значит, гидроизоляционных слоев потребуется меньше (п. 5.5).
Разуклонку можно легко проверить при помощи ведра с водой. Воду выливают на выбранный участок, если вода практически без остатка отойдет к воронке, значить уклон у плоской крыши достаточный. Аналогичную проверку можно провести на всей поверхности крыши.
На стадии проектирования расчетным путем определяется сколько для данной крыши требуется водоприемных воронок, а уже во время строительства при помощи разуклонок необходимо обеспечить для воды беспрепятственный отток в воронку из любой точки крыши.
Как рассчитать уклон кровли: какой способ лучше ↑
Как известно, помимо плоских (пологих) конструкций существуют также скатные и высокие, а материалов для кровельного покрытия еще больше. Для того чтобы правильно сориентироваться в этом многообразии, согласно СНиП разработаны специальные таблицы и диаграммы, в которых отражается взаимосвязь между крутизной ската и видом крыши.
Уклон крыши определяют следующие параметры:
- тип и количество материала, предназначенного для покрытия крыши;
- необходимая защита от ветра и влаги;
- высота конька для случая ремонта уже существующей кровли.
↑Как вычислить угол наклона в градусах и процентах
Рассчитать искомый угол крутизны кровли можно различными способами.
Калькулятор для расчета уклона кровли

Пользоваться данным калькулятором предельно просто. По сути любую кровлю можно разделить на обычные двухскатные, в основе расчета которых лежит треугольник. Именно на этом положении и базируется работа калькулятора. Используются следующие параметры:
- H – высота конька, то есть катет прямоугольного треугольника;
- W – второй катет, равный половине ширины основания;
- L – длина стропил, она же – гипотенуза.
Подставив два известных параметра, можно практически сразу определить угол покатости крыши с подобными характеристиками. Кстати, третий параметр вычисляется автоматически. Программное обеспечение калькулятора использует свойства равнобедренного треугольника и простейшие тригонометрические формулы.
Использование угломера

Этот прибор, который называют еще уклономером, имеет незамысловатую конструкцию: несколько реек с нанесенными делениями и маятник. При расчетах главную рейку располагают перпендикулярно к коньку. На необходимый угол на шкале делений показывает указатель маятника. Как видите, ничего сложного.
Формула расчета уклона кровли
И, наконец, требуемую крутизну ската можно рассчитать самому без использования приборов замера ската, математически. Для этого потребуются знать величину
- вертикальной высоты (H), отмеренной от наивысшей точки ската, обычно это конек, до самой нижней – карниза;
- заложения – горизонтального расстояния от нижней до проекции верхней точки ската.
Рассчитывают угол наклона кровли в градусах или процентах и обозначают на чертеже буквой «i».
Математически расчет величины крутизны крыши в процентах проводят следующим образом.
i = Н : L, т. е. угол уклона крыши находят из отношения высоты кровли к заложению.
После чего, чтобы получить искомую величину в процентах, значение полученного отношения умножают на 100. Выразить значение наклона в градусах помогает специальная таблица соотношений.
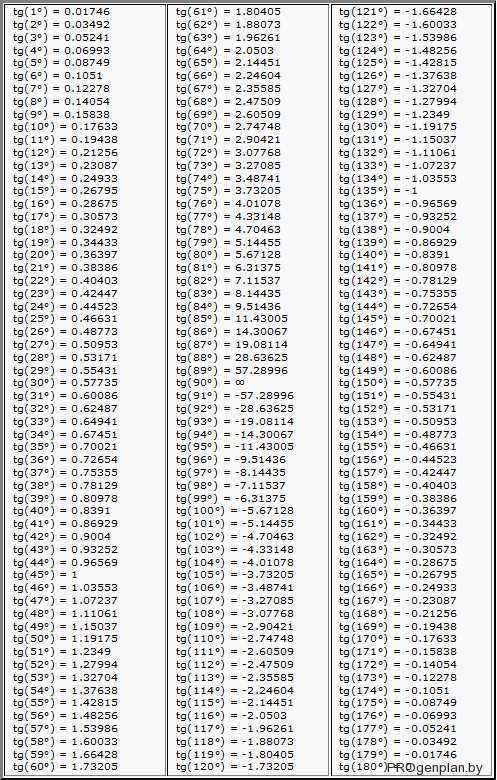
Рассмотрим, как вычислить угол наклона в градусах на конкретном примере.
Пример расчета
Допустим, длина заложения при высоте крыши в 2,5 м оказалась равной 4,5 м.Получается, что уклон i = 2.5 : 4,5 = 0,55. А после умножения 100 получим, соответственно, 55%.
Теперь можно по таблице перевести полученное значение в градусы, получаем — 29°.
Наименьшую крутизну ската для того или иного кровельного покрытия можно определить из следующего графика.
Допустим, речь идет о листовой стали.
- Ищем на графике, в какую наклонную линию упирается дугообразная стрелка 10.
- Точка пересечения наклонной и вертикальной оси дает ответ на поставленный вопрос – самое меньшее 28%.
Пример расчета
Проведем расчеты для конкретного дома.Если H составляет 3 м, а L – 12 м, тогда i = 50%.
Таким образом, в случае приведенных конструктивных размеров необходима крутизна ската в 50% (или 27 градусов), чтобы был обеспечен нормальный сброс дождевой воды.
© 2019 stylekrov.ru
stylekrov.ru
Уклоны. Практика — на уровне глаз — ЖЖ
Часть первая — теоретическая, в которой разбираем, что такое уклонЧасть вторая — техническая, про моделирование уклонов в 3D программах (ArchiCAD и SketchUp)
Часть третья — практическая, примеры из жизни
Время от времени приходится иметь дело с уклонами вообще, и пандусов в частности. «Один к шести», «один к двенадцати», десять процентов, восемь процентов и т.п. Что это? Теоретически это мы разобрали ранее, но хотелось бы знать, как это выглядит в натуре, чтобы понимать как будет «работать» то, что начертишь. В чём разница для «пользователя»? О чём говорят цифры: полого это или круто, удобно или неудобно, и насколько одно отличается от другого?
Пандусы
В СНиПе 31-06-2009 «Общественные здания и сооружения» (п. 5.6) по поводу уклонов пандусов говорится:
Уклон пандусов на путях передвижения людей не должен превышать:
внутри здания, сооружения — 1:6; снаружи — 1:8; на путях передвижения инвалидов на креслах-колясках, в том числе в стационарах лечебных учреждений — от 1:10 до 1:12.
На фото ниже представлены пандусы внутри здания с указанными уклонами — 1:6 и 1:12. Сразу видно, что 1/6 круче, чем 1/12. Заметно круче.
Посмотрели, теперь опишем физические ощущения от ходьбы по данным пандусам, и начнём с малого уклона.
1/12
Он же 8% (i=0,08), он же 4,8°. Это максимально допустимый уклон пандуса для инвалидов, согласно
СНиП 35-01-2001 «Доступность зданий и сооружений для маломобильных групп населения», раздел «Лестницы и пандусы»
п.3.29 Максимальная высота одного подъема (марша) пандуса не должна превышать 0,8 м при уклоне не более 8 %.
Стоит отметить, что там же, в разделе «Участки и территории» указана меньшая цифра:
3.3 Продольный уклон пути движения, по которому возможен проезд инвалидов на креслах-колясках, как правило, не должен превышать 5 %
То есть уклон вне зданий должен быть более пологим. Почему так? Условиями из пункта 3.29 вводятся ограничения в виде перепада высот (0,8 метра) и максимального уклона (8%). При данных условиях максимальная длинна горизонтальной проекции пандуса составит 9,6 метра. В п.3.3 таких ограничений нет, а значит длина может быть любой. Важно, что на удобство перемещения по наклонной плоскости влияет не только величина уклона, но и длинна наклонной поверхности. Поэтому, чем больше длина пандуса, тем меньше должен быть уклон. Даже крутой уклон, преодолеваемый за один шаг, может восприниматься легче, чем более пологий, но продолжительный. Дальнейшие примеры наглядно продемонстрируют, что такое 8% без ограничения длины. Мало не покажется.
Подъём
Переход от ровной поверхности к наклонной почти не заметен, но примерно на шестом шаге инерция горизонтального движения заканчивается, и начинает ощущаться лёгкий подъём.
Спуск
С первого шага отчётливо ощущается изменение характера поверхности (наклон плоскости). При каждом шаге чувствуется небольшой провал.
По ощущениям идти по нему не сложно, но шаг уже явно не такой как по ровной поверхности. Уже вполне отчётливо чувствуется уклон. Если он чувствуется для обычного пешехода, то думаю, что для человека на инвалидной коляске он ощутим очень даже. Подтверждением этого могут быть слова автора книги «Доступная среда глазами инвалида» Елены Геннадьевны Леонтьевой eleont:
Уклон поверхности до 5%, на мой взгляд, можно называть не пандусом, а просто изменением рельефа, выравниванием поверхности, пологим съездом, так как при таком уклоне инвалиду на коляске не требуется посторонняя помощь.
Уклон более 5% вызывает определенные трудности для инвалида на коляске, поэтому необходима установка поручней с двух сторон или помощь сопровождающего.
Архитекторы и проектировщики, имейте это в виду. Если есть возможность заложить в проект более пологий пандус – делайте обязательно. 1/16 (6%) – хорошо, 1/18 – замечательно, 1/20 (5%) – просто великолепно! Прислушайтесь к мнению людей в инвалидной коляске, и не дай нам Бог оказаться на их месте.
Интересно, что при уклоне 1/12 (8%) перепад высоты на один шаг (60 см) составляет 5 см. В нормах тоже фигурируют 5 см.[Нажмите, чтобы прочитать]
СНиП 31-06-2009 «Общественные здания и сооружения», п.5.9. В полу на путях движения не допускаются перепады высотой менее трех ступеней (при высоте ступеней не менее 0,12 м) и пороги выше 0,05 м.
или
СНиП 2.07.01-89* «Градостроительство. Планировка и застройка городских и сельских поселений», п.6.24. В селитебных районах, в местах размещения домов для престарелых и инвалидов, учреждений здравоохранения и других учреждений массового посещения населением следует предусматривать пешеходные пути с возможностью проезда механических инвалидных колясок. При этом высота вертикальных препятствий (бортовые камни, поребрики) на пути следования не должна превышать 5 см; не допускаются крутые (более 100‰) короткие рампы, а также продольные уклоны тротуаров и пешеходных дорог более 50‰. На путях с уклонами 30 — 60‰ необходимо не реже чем через 100 м устраивать горизонтальные участки длиной не менее 5 м.
По моим наблюдениям перепады высотой до 4 см при движении практически не замечаются. А вот 5 см это та крайняя высота, которая уже слабо, но ощущается как препятствие. Его еще явно не переступаешь, но уже нога движется иначе. Колено приподнимается чуть выше, чем при ходьбе по ровной поверхности, и стопа как бы переносится над препятствием.
Почему это так, в какой-то мере можно объяснить тем, что «центр тяжести тела во время Х. совершает движения во всех трёх плоскостях. По вертикали амплитуда его перемещений достигает 4—5 см»— М.: Советская энциклопедия 1969—1978
В связи с этим любопытным представляется, что СНиП 35-01-2001 «Доступность зданий и сооружений для маломобильных групп населения» требует в местах пересечения тротуаров с проезжей частью высоту не более 4 см.
3.4 Высота бортового камня в местах пересечения тротуаров с проезжей частью, а также перепад высот бордюров, бортовых камней вдоль эксплуатируемых газонов и озелененных площадок, примыкающих к путям пешеходного движения, не должны превышать 0,04 м.
Скорее всего, что в данном случае такая цифра вытекает из возможности колеса коляски преодолевать такие перепады высот, а не из-за особенностей ходьбы пешеходов. Хотя Елена Геннадьевна, в своей книге, даёт такой комментарий по этому поводу:
В России почему-то считается, что все инвалиды без исключения могут без проблем преодолеть перепад в 4 см. На самом деле это не так. В международной практике максимально допустимая высота перепада уровней составляет не более 1,3–1,5 см.
Леонтьева Е.Г. Доступная среда глазами инвалида: научно-популярное издание. – Екатеринбург: «БАСКО», 2001. – с.37.
Тем не менее такая норма на руку и пешеходам, так как обеспечивает для них постоянство ритма ходьбы, а значит и её удобство и комфорт.
1/6
Он же 17% (i=0,17), он же 9,5°. Это предельный, максимально допустимый, уклон пандуса для передвижения людей внутри здания, согласно
СНиП 31-06-2009 «Общественные здания и сооружения» п.5.6, который уже воспринимается «горкой». Круче делать нельзя.
Подъём
С первого шага ритм и характер ходьбы меняется — скорее поднимаешься, чем идёшь вперёд. Скорость заметно падает. Шаг короче обычного, тело наклоняется вперёд, чувствуются усилия толчковой ноги. Для придания телу дополнительной динамики в работу включаются руки. Идти по нему не легко, есть ощущение, что по лестнице перемещаться легче. Может быть просто это связано с непривычностью движений, а не с количеством прилагаемых усилий.
Спуск
Чувствуется «тянущая» вперёд сила, для противодействия которой корпус тела отклоняется назад. При каждом шаге но́ги пружинят, и прилагаются усилия для гашения силы ускорения. Иначе шаг легко может перейти в бег.
Дороги
Выше был показан уклон 8% (1/12). Но это было внутри здания, а теперь рассмотрим его снаружи.
Подходящие параметры есть у дороги и тротуаров по пр.Ватутина (от ул.Костюкова до ул.5 Августа), где на перекрёстке пр.Ватутина-ул.Костюкова, в направлении центра города, установлен знак 1.13 «Крутой спуск» с указаным уклоном 9%.

Думаю, что те, кто тут проходил или проезжал уклон этот маленьким не назовут
Как известно, знак указывает лишь угол между началом и концом участка дороги, а в этом промежутке, в каждый отдельный момент, угол может быть разным. Что и показали натурные замеры. Уклон 9% соответствует лишь участку дороги от перекрёстка пр.Ватутина-ул.5 Августа до пешеходного моста. Дальше, до пересечения с ул.Костюкова, уклон равен 8%.
Длина участка с уклоном 8-9% около 250 метров. Не всякий велосипедист осиливает такой подъём, многие идут пешком.
8% Спуск и подъём
Спуск не вызывает особых трудностей, а ощущения при ходьбе были описаны выше. Длительный же подъём, при таком уклоне, даётся не легко. Во время подъёма чувствуется как переставляются ноги, примерно так же, как по лестнице. Обращаешь на это внимание. Мышцы спины начинают выделять тепло. К концу подъёма наблюдается учащённое сердцебиение, увеличивается глубина дыхания и ощущается напряжение мышц ног, в особенности икр.
Если продолжить идти по пр.Ватутина в сторону центра, то на пути встретятся участки с уклонами 5, 7 и 4%
7%
Близко по ощущениям к 8%, но немного легче. Ещё нет глубокого дыхания, учащённого сердцебиения и взмокшей спины. Лёгкий вариант 8%.
5%
Спуск лёгкий, но перемещение уже не совсем «свободное», как при ходьбе по ровной поверхности.
При подъёме чувствуется слабое, еле заметное, приложение усилий, преодоление. Дыхание держится в «нормальном» режиме.
Выводы
Уклон поверхности до 4% включительно не имеет каких-либо существенных различий с ходьбой по горизонтальной поверхности. 5% представляется граничным значением, при котором уже начинают появляться лёгкие изменения в характере ходьбы. Ещё двигаешься без затруднений, но уже различается наклон поверхности. Уклоны больше 5% меняют режим ходьбы, и чем больше уклон, тем изменения заметнее. От величины уклона поверхности зависит расстояние, которое можно пройти без утомления. Чем больше уклон, тем меньше расстояние. Например, при уклоне 2% пройти 1-2 километра не составит труда, а если уклон 8%, то можно запыхаться уже на 150 метрах (при подъёме).
Для объяснения этого можно вспомнить то, что удалось найти по механике ходьбы. Для демонстрации движения человека по наклонной плоскости, я использовал картинку из статьи Адама Саммерса (Adam Summers) «The Biomechanist Went Over the Mountain», размещённой на сайте Natural History Magazine. Повторю её тут.
Данные и картинка © Natural History Magazine
На ней показана последовательность движений человека при ходьбе по ровной поверхности (1), с уклоном 5°(~8%) (2) и уклоном 15°(~26%) (3). Белыми точками обозначено положение общего центра масс (ОЦМ) тела человека, который при ходьбе действует как груз на конце перевёрнутого маятника. Амплитуда перемещений ОЦМ по вертикали составляет 4-5 см, при этом бо́льшая часть энергии (около 65%), затраченной на изменение высоты ОЦМ, сохраняется. Ходьба по плоскости с небольшим уклоном увеличивает затраты энергии на работу маятника, и амплитуду перемещений ОЦМ (2). Часть энергии расходуется на тепло, выделяемое мышцами, а часть всё ещё остаётся для последующих шагов. Но когда уклон становится больше (3), то уже вся энергия тратится на один шаг (так же, как и при восхождении по лестнице).
Отсюда можно вывести ориентировочную классификацию уклонов для пешеходной ходьбы на большие расстояния:
• идеальный 0-2%
• нормальный 2-4%
• допустимый 5-6%
• предельный 7-8%
всё что сверх 8% можно считать затруднительным с различной степенью тяжести.
Таким образом, судя по мои субъективные впечатлениям, увеличение затрат энергии на работу маятника начинается с уклона 5%.
Разница между уклонами в 2% ощущается и различается кинестетически (т.е. суставами и мускулами в движении).
При больших отрезках одного уклона изменения даже в 1% могут быть визуально заметны.
[Инструмент]
Инструмент
Для измерения уклонов использовал самостоятельно изготовленный прибор простой конструкции. Деревянная рейка длиной 1,10 метра (уж какая была), к которой прикреплён плотный картон (3 мм). На нём лист со шкалой и стрелка с грузиком. Можно в качестве стрелки использовать грузик подвешеный на нитке, но в таком случае придётся дольше ждать прекращеня колебаний.
шкала уклономера в процентах pdf, svg
Есть и второй, более современный и компактный, вариант — с помощью приложения Smart Protractor.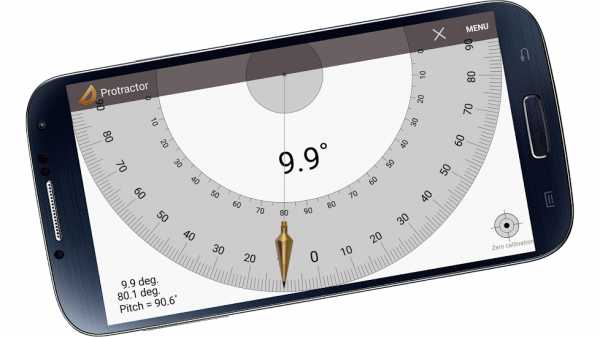
У него в настройках можно выставить показ измерений в радианах, градусах или процентах.
Неплохое приложение, но при измерении малых уклонов, из-за небольшой длины смартфона, точность может быть ±1%, а это многовато. В общем, использовать можно, но для качественного измерения нужно вначале точно откалибровать, а потом желательно сделать несколько замеров и сравнить их с показаниями механического уклономера. Это для понимания условий точного измерения (как держать смартфон, на что ставить, и т.п.)
На этом трилогия «Уклоны» завершена
до этого были:
Часть первая — теоретическая, в которой разбираем, что такое уклон
Часть вторая — техническая, про моделирование уклонов в 3D программах (ArchiCAD и SketchUp)
Напоследок скажу, что всё что описано выше не более чем личные впечатления. Мне это нужно, чтобы в процессе проектирования не только опираться на цифры из нормативных документов, но и иметь кинестетическое представление о них. Также буду признателен, если поделитесь своими впечатлениями, наблюдениями или дополнениями.
© Gre-kow, 2015. gre-kow.livejournal.com
При копировании активная ссылка http://gre-kow.livejournal.com/26916.html обязательна
gre-kow.livejournal.com
