Уклон 5 процентов сколько градусов. Что означает уклон в процентах, и как перевести его в градусы
Уклон скатов крыши — от чего зависит и в чём он измеряется.
Такой немаловажный для крыши факт — её уклон. Уклон крыши — это угол наклона кровли относительно горизонтального уровня. По углу наклона скатов крыши бывают малоуклонные (пологие), средней наклонности и крыши с крутыми (сильноуклонными) скатами .
Малоуклонная крыша та крыша , монтаж которой осуществляется из расчёта наименьшего, рекомендованного угла наклона скатов. Так для каждого кровельного покрытия есть свой рекомендуемый минимальный уклон.
От чего зависит уклон кровли
- От способности крыши защищать строение от внешних факторов и воздействий.
- От ветра — чем больше уклон крыши, тем больше значение приходящихся ветровых нагрузок. При крутых уклонах уменьшается сопротивляемость ветру, повышается парусность. В регионах и местах с сильными ветрами рекомендуется применять минимальный уклон крыши, чтоб уменьшить нагрузки на несущие конструкции крыши.
- От кровельного покрытия (материала) — Для каждого кровельного материала существует свой минимальный угол наклона, при котором можно использовать данный материал.
- От архитектурных задумок, решений, местных традиций — так в разных регионах отдаётся предпочтение для той или иной конструкции крыши.
- От атмосферных осадков : снеговых нагрузок и дождей в регионе. На крышах с большим уклоном не будет скапливаться в огромных количествах снег, грязь и листья.
В чем измеряется угол уклона крыши
Обозначение уклона кровли на чертежах может быть как в градусах, так и в процентах. Уклон крыши обозначается латинской буквой i .
В СНиПе II-26-76, данная величина указывается в процентах (%). В данный момент не существует строгих правил по обозначению размера уклона крыши.
Единицей измерения уклона крыши считают градусы или проценты (%). Их соотношение указаны ниже в таблице.
Уклон крыши соотношение градусы-проценты
| градусы | % | градусы | % | градусы | % | ||
| 1° | 1,75% | 16° | 28,68% | 31° | 60,09% | ||
| 2° | 3,50% | 17° | 30,58% | 32° | 62,48% | ||
| 3° | 5,24% | 18° | 32,50% | 33° | 64,93% | ||
| 4° | 7,00% | 19° | 34,43% | 34° | 67,45% | ||
| 5° | 8,75% | 20° | 36,39% | 35° | 70,01% | ||
| 6° | 10,51% | 21° | 38,38% | 36° | 72,65% | ||
| 7° | 12,28% | 22° | 40,40% | 37° | 75,35% | ||
| 8° | 14,05% | 23° | 42,45% | 38° | 78,13% | ||
| 9° | 15,84% | 24° | 44,52% | 39° | 80,98% | ||
| 10° | 17,64% | 25° | 46,64% | 40° | 83,90% | ||
| 11° | 19,44% | 26° | 48,78% | 41° | 86,92% | ||
| 12° | 21,25% | 27° | 50,95% | 42° | 90,04% | ||
| 13° | 23,09% | 28° | 53,18% | 43° | 93,25% | ||
| 14° | 24,94% | 29° | 55,42% | 44° | 96,58% | ||
| 15° | 26,80% | 30° | 57,73% | 45° | 100% |
Перевести уклон из процентов в градусы и наоборот из градусов в проценты можно при помощи онлайн конвертера:
Замер уклона крыши
Измеряют угол уклона при помощи уклономера или же математическим способом.
Уклономер — это рейка с рамкой, между планками которой есть ось, шкала деления и к которой закреплён маятник. Когда рейка находится в горизонтальном положении, на шкале показывает ноль градусов. Чтобы произвести замер уклона ската крыши, рейку уклономера держат перпендикулярно коньку, то есть в вертикальном уровне. По шкале уклономера маятник указывает, какой уклон у данного ската крыши в градусах. Такой метод замера уклона стал уже менее актуален, так как сейчас появились разные геодезические приборы для замеров уклонов, а так же капельные и электронные уровни с уклономерами.
Математический расчёт уклона
- Вертикальная высота (H ) от верхней точки ската (как правило конька) до уровня нижней (карниза)
- Заложение ( L ) — горизонтальное расстояние от нижней точки ската до верхней
lkrservice.ru
как посчитать, методы, как перевести градусы в промилле
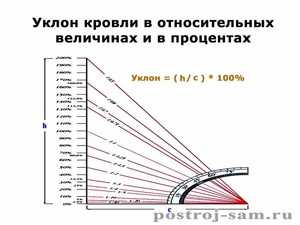Существуют нормативы на уклоны при проектировании различных коммуникаций и сооружений, которыми руководствуются в своей работе архитекторы и строители. Пользоваться можно любыми размерностями, в том числе и градусами. На практике принято крутые склоны обозначать в градусах, а пологие — в процентах и промилле.
Способы вычисления склона в процентах
При выполнении планировочных работ на земельном участке приходится прибегать к измерениям крутизны косогоров. Сделать это можно несколькими методами:
С помощью нивелира выполняются все необходимые измерения, а потом несложными вычислениями формируется уклон в процентах. Как считать: перепад высот делится на расстояние между точками замеров, и результат умножается на сто процентов.- По плану земельного участка, если на нём вынесены отметки рельефа местности. Разница высот между необходимыми точками считывается с рисунка, а расстояние замеряется масштабной линейкой. Дальнейшие вычисления аналогичны предыдущему способу.
С помощью нивелира выполняются все необходимые измерения, а потом несложными вычислениями формируется уклон в процентах. Как считать: перепад высот делится на расстояние между точками замеров, и результат умножается на сто процентов.Кровельщики часто сталкиваются с необходимостью определить фактический скат крыши, и знают, как рассчитать уклон с помощью специального инструмента, называемого уклономер. Конструкция приспособления несложная: на рейке закреплена рамка с закреплённым внутри транспортиром и маятником, имеющим груз и указатель.
Определение угла наклона через тангенс
Из тригонометрии известно, что тангенс — дробь, в основании которой прилежащий к углу катет, а поверх — противолежащий (перепад высот). Чтобы определить уклон кровли в процентах и градусах через тангенс, понадобится выполнить замеры:
- высоты от потолочного перекрытия до конька кровли;
- расстояния от края ската до проекции верхней линии смыкания двух плоскостей.
Сделав несложные расчёты, получают некоторое значение и по таблице Брадиса или с помощью инженерного калькулятора находят соответствующее число градусов для искомого угла. Как посчитать уклон в процентах — определено выше: высоту конька делят на половину ширины чердачного перекрытия, если скаты равной величины. Или на проекцию каждой из поверхностей кровли, когда размеры сторон различаются. Можно заметить, что это и есть тангенс уже определённого в градусах угла. Чтобы перейти к процентному выражению уклона, надо выполнить действие: значение tg *100, и результат получится в процентах.
Соотношение величин с уклоном крыши
Для каждого кровельного материала установлены допуски по наименьшему уклону. Другие факторы, влияющие на выбор угла скатов крыши:
- способность комплексно защищать строение от внешних воздействий — техногенных и природных;
- стойкость к ветровой нагрузке — крутые поверхности увеличивают парусность сооружения, это делает конструкцию уязвимой;
- преобладание определённых решений архитекторов в отдельных регионах;
- количество атмосферных осадков и загрязнений — на кровле с большим уклоном груз накапливаться не будет.
способность комплексно защищать строение от внешних воздействий — техногенных и природных;Строительные нормы и правила — СНиП II -26−76 регламентируют пологость скатов в процентах. Соотношение процентов и градусов для некоторых углов приведено в таблице.
| Градус º | Тангенс | Процент, % | Промилле, ‰ | Градус º | Тангенс | Процент, % | Промилле, ‰ |
| 1 | 0,0175 | 1,75 | 17,5 | 22 | 0,4040 | 40,40 | — |
| 5 | 0,0875 | 8,75 | 87,5 | 24 | 0,4452 | 44,52 | — |
| 10 | 0,1740 | 17,40 | 174 | 26 | 0,4878 | 48,78 | — |
| 12 | 0,2125 | 21,25 | — | 28 | 0,5318 | 53,18 | — |
| 14 | 0,2494 | 24,94 | — | 30 | 0,5773 | 57,73 | — |
| 16 | 0,2868 | 28,68 | — | 35 | 0,7001 | 70,01 | — |
| 18 | 0,3250 | 32,50 | — | 40 | 0,8390 | 83,90 | — |
| 20 | 0,3828 | 38,28 | — | 45 | 1,0000 | 100,0 | — |
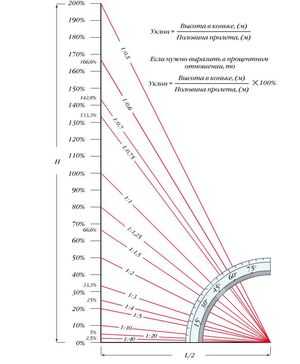Математические способы расчёта уклона применяются, когда особая точность не нужна, и измерения делают приблизительные. При необходимости вычислить точные показатели, пользуются современными измерительными приборами.
Пример вычисления: расстояние от края ската кровли до проекции линии сопряжения сторон — длина заложения, 5,2 м. Высота от чердачного перекрытия до верхней отметки кровли 2 метра. Уклон (тангенс угла) определяется действием: 2/5,2 = 0,3846. Ближайшее значение из таблицы — 20 градусов, что соответствует примерно 38%.
Другой вариант — с помощью угломера определили угол наклона кровли, его значение 5º. По соответствующей строке уклон поверхности составит 8,75 процента или 87,5 промилле.
planken.guru
Угол уклона пандуса
Основным нормативным документом для определения уклона пандуса и его длины в РФ является СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» С Изменением №1 — актуализированная версия СНиП 35-01-2001.
Допустимые значения угла наклона пандуса
— Допустимый угол уклона пандуса должен быть не круче 1:20 (5%), а максимальная высота одного подъема (марша) пандуса не должна превышать 0,8 м.— При перепаде высот пола на путях движения 0,2 м и менее допускается увеличивать уклон пандуса до 1:10 (10%)
— На временных сооружениях или объектах временной инфраструктуры допускается максимальный уклон пандуса 1:12 (8%) при условии, что подъем по вертикали между площадками не превышает 0,5 м, а длина пандуса между площадками — не более 6,0 м.
— Пандусы при перепаде высот более 3,0 м и расчетной длиной более 36 м следует заменять лифтами, подъемными платформами и т.п
— В соответствии с приказом Минстроя России №750/пр от 21 октября 2015 г. «Об утверждении изменений №1 к СП 59.13330.2012 «Доступность зданий и сооружений для маломобильных групп населения» «При проектировании реконструируемых, подлежащих капитальному ремонту и приспосабливаемых существующих зданий и сооружений уклон пандуса принимается в интервале от 1:20 (5%) до 1:12 (8%)».
Что обозначают цифры
1:10 — 10% — один к десяти, т.е. при перепаде высот в 1 м, длина пандуса должна быть 10 м, при высоте 0,5 м — длина пандуса должна быть 5 м и т.д.
В этом случае угол уклона пандуса будет соответствовать 5,7 градусам.
1:12 — 8% — один к двенадцати, т.е. при перепаде высоты в 1 м, длина пандуса должна быть 12 м, при высоте 0,5 м — длина пандуса должна быть не менее 6 метров и т.д.
Угол уклона пандуса будет равен 4,8 градусам.
1:20 — 5% — один к двадцати, т.е. при перепаде высот 1 м, длина пандуса должна быть 20 м, при высоте 0,5 м — 10 м.
Угол уклона пандуса будет равен 2,9 градусам.
Какой длины делать пандус?
|
Расчет длины пандуса в зависимости от высоты |
|||
|
Высота пандуса, м |
Длина пандуса, м |
||
|
1:10=10%=5,7° (используется при перепаде высот менее 0,2 м) |
1:12=8%=4,8° (для временных, приспосабливаемых и реконструируемых сооружений) |
1:20=5%=2,9° (стандартный показатель) |
|
|
0,1 |
1 |
1,2 |
2 |
|
0,2 |
2 |
2,4 |
4 |
|
0,3 |
3 |
3,6 |
6 |
|
0,4 |
4 |
4,8 |
8 |
|
0,5 |
5 |
6 |
10 |
|
0,6 |
6 |
7,2 |
12 |
|
0,7 |
7 |
8,4 |
14 |
|
0,8 |
8 |
9,6 |
16 |
|
0,9 |
9 |
10,8 |
18 |
|
1 |
10 |
12 |
20 |
|
1,1 |
11 |
13,2 |
22 |
|
1,2 |
12 |
14,4 |
24 |
|
1,3 |
13 |
15,6 |
26 |
|
1,4 |
14 |
16,8 |
28 |
|
1,5 |
15 |
18 |
30 |
Зеленый — допустимые значения, красный — недопустимые.
Если Вам необходимо самостоятельно рассчитать угол уклона пандуса, зная его длину и высоту, то необходимо воспользоваться следующей формулой
arcsin(h/L), где h — высота, L — длина.
Для этого
воспользуйтесь инженерным калькулятором
Примеры внедрений
www.pandus-msk.ru
Уклон в градусах и процентах
Горнолыжные градиенты или о крутизне синих, красных и черных трасс
Поговорим об уклонах
На практике крутизна наклонной поверхности в различных областях человеческой деятельности обозначается величиной уклона (или еще иначе — градиентом). Для начала давайте разберемся, что же означает само это понятие. Таблички с указанием уклона знакомы, наверное, всем водителям автомобилей (по крайней тем, кто самостоятельно сдал хотя бы теорию), но далеко не все из них знают, что же фактически означает, например, 10% на знаке.
Кто-то по-простому думает, что это угол наклона дороги, то есть 10 градусов. Некоторые идут дальше в своих размышлениях и считают, что это доля от максимально возможного угла подъема в 90 градусов (отвесная стена) и 10% — это 90°×0.1 = 9°. Мы все привыкли мыслить в градусах, каждый может визуально представить себе 90 градусов, 45, 30 и т.д., поэтому и стремимся все воспринимать в этой единице измерения (а правильный ответ: 10% = 5.7°).
На самом деле математически уклон — это отношение перепада высоты на определенном участке пути к длине горизонтальной проекции этого пути, выраженное в процентах. Т.е. высота (h), разделенная на проекцию пути (c) и умноженная на 100. Геометрически это отношение противолежащего катета к прилежащему (тангенс, умноженный на 100). Таким образом:
Уклон в процентах (градиент) = h/c×100 = tg(a)×100
Ниже представлена форма, позволяющая перевести значения из градиентов в градусы и обратно:
Градиенты % = Градусы °
Ближе к делам горнолыжным
С теорией разобрались, переходим к горнолыжной практике.
Профиль горнолыжной трассы никогда не представляет из себя идеальную прямую. Где-то наклон может быть покруче, где-то поположе.
Уклон кровли в градусах и процентах
В этом случае используется понятие среднего градиента, который, впрочем, вычисляется все по той же формуле: перепад высот между стартом и финишем трассы, деленный на длину горизонтальной проекции трассы.
По статистике средние градиенты синих трасс находятся в пределах до 18% (порядка 10 градусов), красных — до 23% (13 градусов), а черных — от 23% и выше (больше 13 градусов). На каких-то курортах сложность трасс несколько занижена (синие трассы в реальности могут оказаться ближе к красным по крутизне), на каких-то наоборот, ее завышают, но в среднем картина везде примерно такая.
Для ориентировочной оценки длин трасс, катаясь на курорте и имея на руках схему катания с обозначением перепадов высот, вы можете использовать следующие соотношения:
На каждый километр перепада высоты синей трассы приходится порядка 7 км ее длины, на километр перепада красной — 5 км, черной — 3.5 км.
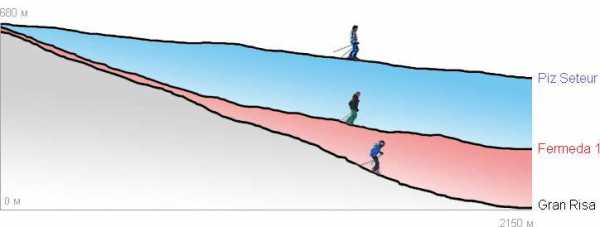
Ниже на картинке для сравнения представлены профили синей, красной и черной трасс. Трассы находятся в известнейшем итальянском регионе Селларонда, а профили их взяты из замечательного приложения 3D Dolomiti Superski, которое позволяет совершить виртуальный тур по региону, а также посмотреть технические характеристики всех трасс.
| Название трассы | Длина | Перепад | Наклон | Градиент |
|---|---|---|---|---|
| Piz Seteur | 2050 м | 204 м | 5.7° | 10.0% |
| Fermeda 1 | 2090 м | 456 м | 12.6° | 22.4% |
| Gran Risa | 2290 м | 677 м | 17.2° | 30.9% |
Отдельно отметим представленную на картинке Gran Risa — знаменитую трассу, входящую в пятерку культовых трасс Кубка мира. Глядя на ее профиль можно подумать, что ничего такого особенного в нем нет, но на деле, когда вы оказываетесь на трассе, в некоторых местах может показаться, что склон уходит вертикально вниз.
Этот эффект часто присутствует при сравнении профиля трассы с реальной обстановкой на местности. Также не будем забывать, что мы все время ведем речь о средних градиентах, в то время как некоторые локальные участки склона могут оказаться намного круче (и часто именно по этим самым крутым местам присваивают сложность трассе).
Харакири
В австрийском Майрхофене находится одна из самых крутых трасс мира (и самая крутая в Австрии), с говорящим названием Harakiri. Ее средний уклон составляет 78% (38°, длина около 620 метров при перепаде 380 метров). Для подготовки склона используется специальная техника, закрепленная на спущенных сверху страховочных канатах.
Падение на Harakiri может быть чревато тем, что до конца трассы вы будете катиться кубарем, не имея возможности затормозить.
Так что всегда, катаясь на лыжах, соизмеряйте свои возможности с предлагаемыми горами условиями. Берегите себя и окружающих лыжников!
  При решении геодезических и инженерных задач, очень часто приходиться вспоминать и искать необходимые формулы. В связи с этим хочется представить Вам шпаргалку (назовем её “геодезической шпаргалкой”:)), в которой приведены часто использующиеся формулы.
  Конечно, ее содержание не охватывает всю высшую математику или сферическую геометрию, но что-нибудь должно пригодиться.
  Зная из собственного опыта, неудобство восприятия формул без чисел, к каждой из них приводится пример вычисления.
Пример вычислений теорема Пифагора
Пример вычислений соотношения в прямоугольном треугольнике
— арксинус (arcsin) возвращает угол по его синусу
— арккосинус (arccos) возвращает угол по его косинусу
— арктангенс (arctg) возвращает угол по его тангенсу
— арккотангенс (arcctg) возвращает угол по его арктангенсу
Пример вычислений обратные тригонометрические функции
Сумма углов в треугольнике равна 180 градусам
Для любого треугольника соблюдается выражение
Пример вычислений теорема синусов
  Квадрат любой стороны треугольника, равен сумме квадратов двух других его сторон, минус удвоенное произведение этих сторон на косинус угла между ними
Пример вычислений теорема косинусов
  Площадь треугольника можно определить по формулам
также удобно использовать формулу Герона , где p-полупериметр треугольника
Пример вычислений площадь треугольника
или по формуле Герона
  Длина дуги окружности вычисляется по формулам
если угол задан в угловых градусах минутах и секундах
если угол задан в радианах
Пример вычислений длина дуги окружности
угол задан в угловых градусах минутах и секундах
угол задан в радианах
  Перевод угловых градусов минут и секунд в градусы выполняется согласно выражения
Пример вычислений
перевести в градусы угол, который задан в угловых градусах минутах и секундах
Смотрите перевод минут и секунд угла в градусы онлайн   Перевод градусов в угловые градусы минуты и секунды выполняется согласно выражения
Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в градусах
Смотрите перевод градусов угла в минуты и секунды онлайн   Перевод градусов в радианы выполняется по формуле
Пример вычислений
перевести в радианы угол, который задан в угловых градусах минутах и секундах
Смотрите перевод градусов в радианы онлайн   Перевод радианов в градусы выполняется по формуле
Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в радианах
Смотрите перевод радиан в градусы онлайн   Определение наклона линии в градусах выполняется с использованием соотношений в прямоугольном треугольнике Пример вычислений
  Определить наклон пандуса длиной 14м и высотой 3,5м
  При инженерно-строительных работах, наклон линии задают не градусом наклона, а тангенсом этого градуса — безразмерной величиной, которая называется уклоном. Уклон может выражаться относительным числом, в процентах (сотые доли числа) и промилле (тысячные доли числа)
Пример вычислений
  Определить уклон отмостки длиной 2,5м и высотой 0,30м
astgift.ru
| 1 | Вычислить | 2+2 | |
| 2 | Вычислить | 2^3 | |
| 3 | Вычислить | 4^2 | |
| 4 | Разложить на простые множители | 73 | |
| 5 | Вычислить | 6/2(1+2) | |
| 6 | Найти объем | сфера (5) | |
| 7 | Найти площадь | окружность (5) | |
| 8 | Вычислить | корень четвертой степени -625 | |
| 9 | Вычислить | -5^2 | |
| 10 | Вычислить | 2^4 | |
| 11 | Найти площадь поверхности | сфера (5) | |
| 12 | Вычислить | -3^2 | |
| 13 | Вычислить | 2^5 | |
| 14 | Вычислить | 6÷2(1+2) | |
| 15 | Вычислить | 3^2 | |
| 16 | Преобразовать в десятичную форму | 1/4 | |
| 17 | Вычислить | (-3)^3 | |
| 18 | Вычислить | -2^2 | |
| 19 | Вычислить | 2^2 | |
| 20 | Вычислить | 6^2 | |
| 21 | Вычислить | квадратный корень 3* квадратный корень 12 | |
| 22 | Вычислить | (-4)^2 | |
| 23 | Вычислить | -7^2 | |
| 24 | Преобразовать в десятичную форму | 3/4 | |
| 25 | Преобразовать в десятичную форму | 7/8 | |
| 26 | Вычислить | квадратный корень 28+ квадратный корень 63 | |
| 27 | Преобразовать в десятичную форму | 2/3 | |
| 28 | Найти площадь | окружность (7) | |
| 29 | Найти площадь | окружность (2) | |
| 30 | Вычислить | 8^2 | |
| 31 | Разложить на простые множители | 6 | |
| 32 | Преобразовать в обыкновенную дробь | 0.75 | |
| 33 | Вычислить | — корень четвертой степени 625 | |
| 34 | Найти площадь | окружность (4) | |
| 35 | Преобразовать в десятичную форму | 3/8 | |
| 36 | Вычислить | 4^3 | |
| 37 | Разложить на простые множители | 8 | |
| 38 | Вычислить | 5^3 | |
| 39 | Преобразовать в десятичную форму | 3/8 | |
| 40 | Найти площадь | окружность (6) | |
| 41 | Преобразовать в десятичную форму | 3/4 | |
| 42 | Вычислить | (-4)^3 | |
| 43 | Вычислить | 3^3 | |
| 44 | Разложить на простые множители | 4 | |
| 45 | Найти объем | сфера (4) | |
| 46 | Перевести в процентное соотношение | 1/8 | |
| 47 | Найти площадь | окружность (3) | |
| 48 | Преобразовать в десятичную форму | 2/5 | |
| 49 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 50 | Вычислить | 5^2 | |
| 51 | Вычислить | (-2)^4 | |
| 52 | Разложить на простые множители | 2 | |
| 53 | Вычислить | корень четвертой степени 256 | |
| 54 | Вычислить | квадратный корень 81 | |
| 55 | Преобразовать в десятичную форму | 1/2 | |
| 56 | Вычислить | -4^2 | |
| 57 | Вычислить | -9^2 | |
| 58 | Вычислить | (-5)^2 | |
| 59 | Вычислить | (-8)^2 | |
| 60 | Разложить на простые множители | 741 | |
| 61 | Разложить на простые множители | 9 | |
| 62 | Найти объем | сфера (3) | |
| 63 | Вычислить | 3 квадратный корень 8*3 квадратный корень 10 | |
| 64 | Найти площадь | окружность (10) | |
| 65 | Найти площадь | окружность (8) | |
| 66 | Вычислить | -8^2 | |
| 67 | Вычислить | (-5)^3 | |
| 68 | Вычислить | (-2)^3 | |
| 69 | Вычислить | 10^6 | |
| 70 | Вычислить | 10^2 | |
| 71 | Вычислить | -6^2 | |
| 72 | Преобразовать в десятичную форму | 1/5 | |
| 73 | Преобразовать в десятичную форму | 4/5 | |
| 74 | Преобразовать в десятичную форму | 10% | |
| 75 | Найти площадь поверхности | сфера (6) | |
| 76 | Перевести в процентное соотношение | 3/5 | |
| 77 | Вычислить | (-2)^2 | |
| 78 | Разложить на простые множители | 12 | |
| 79 | Разложить на простые множители | 1162 | |
| 80 | Вычислить | 6^3 | |
| 81 | Вычислить | -3^4 | |
| 82 | Вычислить | 2^2 | |
| 83 | Вычислить | (-6)^2 | |
| 84 | Вычислить | (-7)^2 | |
| 85 | Найти площадь | окружность (1) | |
| 86 | Преобразовать в десятичную форму | 2/5 | |
| 87 | Вычислить | квадратный корень 2+ квадратный корень 2 | |
| 88 | Вычислить | 2^1 | |
| 89 | Вычислить | 2^6 | |
| 90 | Разложить на простые множители | what is the prime factoriztion of 40 use exponents to show any repeated prime factors | what is the prime factoriztion of use exponents to show any repeated prime factors |
| 91 | Вычислить | -2^3 | |
| 92 | Вычислить | 3^5 | |
| 93 | Вычислить | (-9)^2 | |
| 94 | Вычислить | 4^1 | |
| 95 | Вычислить | квадратный корень 100 | |
| 96 | Преобразовать в десятичную форму | 25% | |
| 97 | Найти длину окружности | окружность (5) | |
| 98 | Найти площадь поверхности | сфера (6) | |
| 99 | Найти объем | сфера (2) | |
| 100 | Найти объем | сфера (6) | |
www.mathway.com
Уклон (геодезия) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Уклон. Уклон поверхности равен тангенсу угла α, tgα = h/l — отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра Дорожный знак 1.14 «Крутой подъём»Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается. Иными словами, величина уклона равна тангенсу угла между величиной подъёма склона и горизонталью (тангенсу угла наклона).
Например, подъёму 12 метров на 100 метров перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰)[1][2][3][4].
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».
Уклон указывают на дорожных знаках 1.13 «Крутой спуск» и 1.14 «Крутой подъём»[5].
На топографическом плане (карте) уклон можно определить по графику заложений уклонов.
- ↑ Н. Н. Васильев, О. Н. Исаакян, Н. О. Рогинский, Я. Б. Смолянский, В. А. Сокович, Т. С. Хачатуров. Технический железнодорожный словарь. — Москва: Государственное транспортное железнодорожное издательство, 1941. — 608 с.
- ↑ Александр Михайлович Прохоров. Большой энциклопедический словарь. — Научное изд-во «Большая Российская энциклопедия», 2000. — 1456 с.
- ↑ Алексей Владимирович Скворцов, Павел Иванович Поспелов, Андрей Александрович Котов. Геоинформатика в дорожной отрасли. — Алексей Владимирович Скворцов, 2005-07-05. — С. 129. — 252 с.
- ↑ С. К. Боголюбов. Черчение. — Рипол Классик. — С. 41. — 339 с. — ISBN 9785458308199.
- ↑ Р. Мубаракшин. Знаете ли вы дорожные знаки? Все про дорожные знаки и разметку. Редакция 2019 года. — Litres, 2018-10-01. — С. 9. — 99 с. — ISBN 9785457656154.
ru.wikipedia.org
Как рассчитать поперечный и продольный уклоны? — PROGENPLAN
Нормативные требования по уклонам
При проектировании улиц населенных пунктов необходимо соблюдать требования по минимальным и максимальным показателям продольных и поперечных уклонов. Значения уклонов приводятся в промилле.
Поперечный уклон проезжей части улиц и площадей принимается в зависимости от типа дорожного покрытия:
— асфальтобетонные и цементобетонные – 15 ‰ — 25 ‰;
— сборные из бетонных и железобетонных плит, брусчатые мостовые — 20 ‰ — 25 ‰;
— щебеночные и гравийные — 20 ‰ — 30 ‰;
— булыжные мостовые — 20 ‰ — 35 ‰.
При возведении и реконструкции в стесненных условиях можно увеличить поперечные уклоны на 5 ‰.
Поперечные и продольные уклоны машино-места на площадках автостоянок и парковок принимается в пределах от 5 ‰ до 40 ‰.
Поперечный уклон машино-места на парковках, прилегающих непосредственно к проезжей части улиц, допускается увеличивать до 60 ‰.
Минимальный продольный уклон на улицах со стоком поверхностных вод, осуществляемым
по лоткам вдоль проезжей части, следует принимать:
— для асфальтобетонных и цементобетонных покрытий — 4 ‰;
— для остальных типов покрытий — 5 ‰.
Если водоотводные лотки вдоль проезжей части не предусматриваются, то значение минимального продольного уклона не нормируется, и он обеспечивается за счет поперечных уклонов.
Продольные уклоны на участках улиц с движением автобусов, троллейбусов и трамваев не должны превышать:
— 60 ‰ — с остановочными пунктами и радиусами кривых в плане 250 м и более;
— 40 ‰ — с остановочными пунктами и радиусами кривых в плане от 100 до 250 м;
— 40 ‰ — без остановочных пунктов с радиусами кривых в плане менее 100 м.
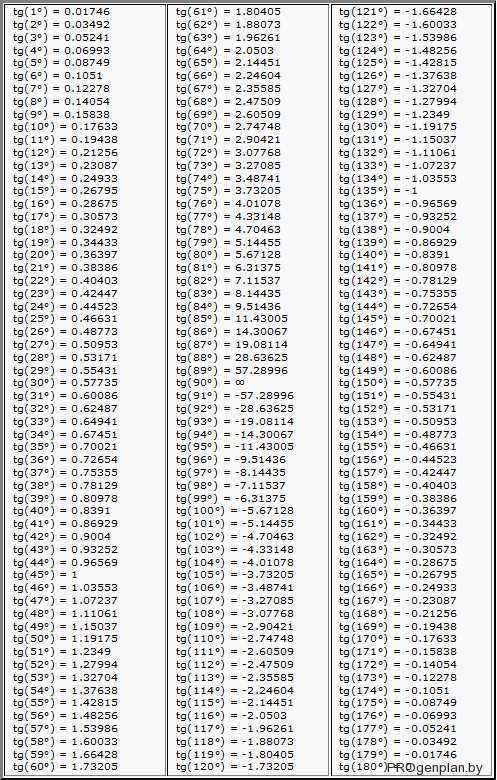
Перевод промилле в градусы
При переводе промилле в градусы можно пользоваться таблицей Брадиса. Для этого нужно поделить количество промилле на 1000 – это тангенс угла, и посмотреть в таблице значение угла в градусах.
Но куда проще и быстрее воспользоваться онлайн конвертером величин (откроется в новой вкладке).
При помощи таблицы Брадиса можно выполнить и обратную задачу – перевести градусы в промилле. Например, значение 50 по таблице = 0,08749. Если умножим это значение на 100, то получим проценты (8,749%), а умножим на 1000 – получим промилле (87,49‰).
Расчет продольного уклона
Чтобы проверить, соответствует ли запроектированное значение продольного уклона нормативным показателям, можно выполнить небольшой расчет:
Разницу проектных отметок поделить на расстояние между этими отметками и умножить на 1000. Получите значение уклона в промилле.
Пример:
179.04 — 178.93 = 0,11; 0,11/15,2м*1000 = 7,2 ‰.
Расчет поперечного уклона
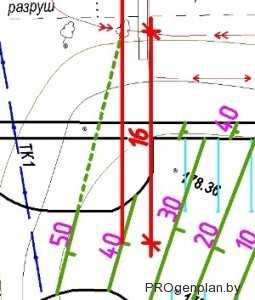Запроектированное значение поперечного уклона проверим с помощью двух выбранных горизонталей. С середины одной из выбранных горизонталей проводим перпендикуляр. Продлеваем другую горизонталь до перпендикуляра.Длина получившейся линии (от начала перпендикуляра до точки пересечения) равна 16м. как на рисунке. Зная превышение и расстояние просчитываем поперечный уклон – ( 0,1м : 16м) * 1000= 6,3 ‰.
progenplan.by